NumPy 랑 친해지기

Posted Aug 31, 2025 Updated Oct 9, 2025

By figure.2

42 min read

NumPy 랑 친해지기

🦥 본문

💡 import numpy as np

위 구문으로 NumPy 를 사용한다고 전제한다.

⭐ 설치 및 환경

가상환경은 pyenv 와 pyenv 의 virtualenv 플러그인을 사용해서 만들었다.
- pyenv 설치 및 사용법은 이 문서를 참고하는 것이 좋다.
Python: 3.12.7
Numpy: 2.2.4

아래의 명령어를 사용해서 numpy 를 설치하고 실습을 진행했다.

  
pip install numpy==2.2.4

🎲 ndarray

n-dimension array 라는 의미! 즉, 다차원 배열을 표현하는 데이터 타입
ndarray 는 수학의 vector 와 matrix 개념을 python 에서 효율적으로 표현하기 위한 데이터 타입
내부 구현은 CPython 으로 구현되어있어 속도가 매우 빠르고 메모리 관리가 효율적
python 의 list 와는 다르다!

dimension 은 axis (축)

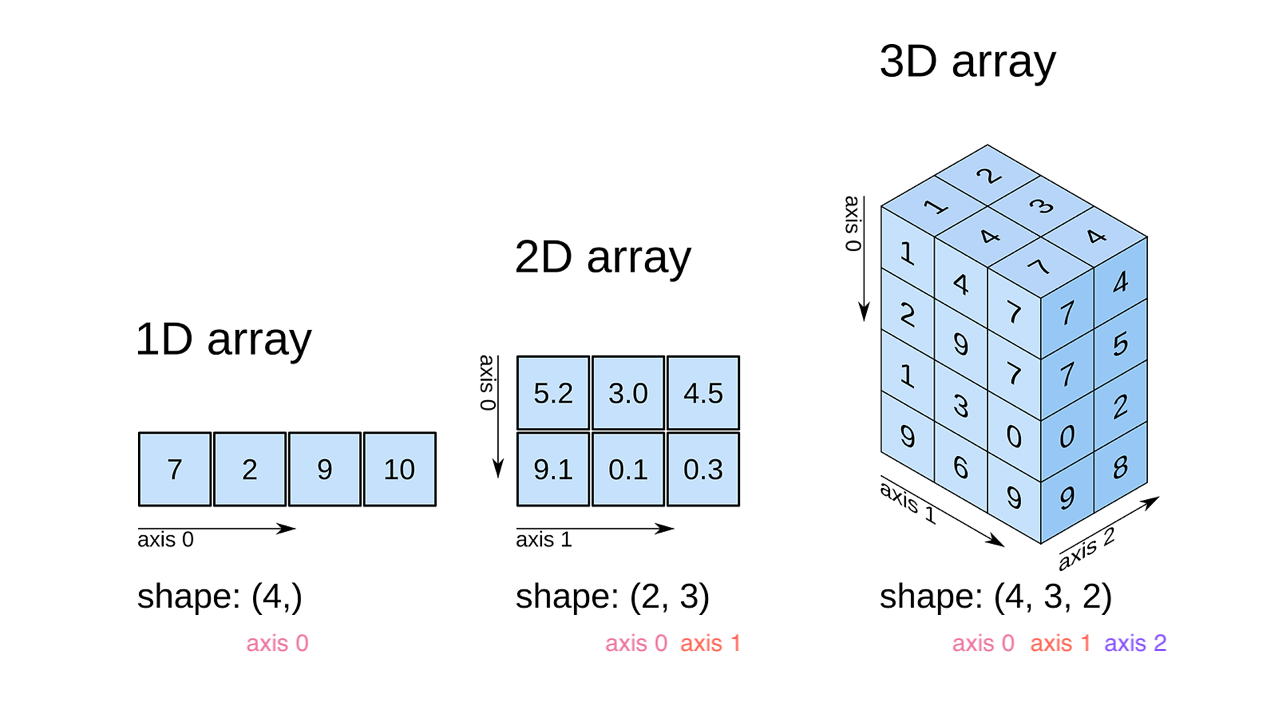
ndarray 의 모양을 나타낼 때, shape 이라는 말을 사용하고, (axis 0 의 item 수, … , axis n 의 item 수) 라는 tuple 을 보여준다.
예시)
- 1D array; shape:(갯수, )
- 2D array; shape:(갯수, 갯수)
- 3D array; shape:(갯수, 갯수, 갯수)
tuple 이 아무리 길어도 index 번호가 곧 axis 번호. 즉, 마지막 2차원이 매우 익숙한 2차원 배열!

대표적인 attributes

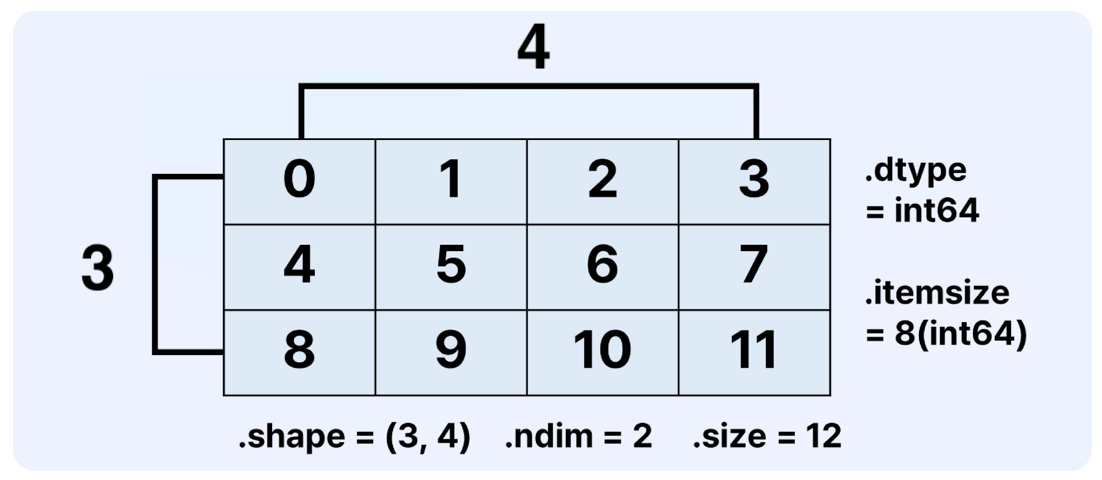
shape: 각 축의 크기를 tuple 로 표현한 속성. ex.) (4, 3, 2)
ndim: 차원의 개수
dtype: 요소(Element) 의 data type. (ndarray 는 1개의 데이터 타입만 갖는다.)
itemsize: 요소(Element) 의 bytes. ex.) dtype 이 int64 라면, itemsize 는 8(bytes) 이다.
size: 전체 요소(Element) 개수

다양한 생성 방법

기본적으로는, numpy 의 array(list 또는 tuple) 함수로 생성할 수 있다.

  
import numpy as np

a = np.array((1, 2, 3, 4))  # shape: (4,) | ndim: 1 | dtype: int64 | itemsize: 8 | size: 4
b = np.array([[0, 1], [1, 0]])  # shape: (2, 2) | ndim: 2 | dtype: int64 | itemsize: 8 | size: 4
c = np.array([1.2, 3.14, 7.0])  # shape: (3,) | ndim: 1 | dtype: float64 | itemsize: 8 | size: 3

실무에서 자주 쓰이는 방법은 다음과 같다.

np.zeros(shape): 0 으로 구성된 N 차원 배열. ex.) np.zeros((3, 4))
np.ones(shape): 1 로 구성된 N 차원 배열. ex.) np.ones((10, ))
np.empty(shape): 초기화되지 않은 N 차원 배열. ex.) np.empty((1, 3, 4))

arange 로 ndarray 만들기

array range 의 줄임말로, N 만큼 차이나는 숫자로 1 차원 ndarray 를 만들어준다.

function signature, 그러니까 함수 프로토타입은 아래와 같다.

  
np.arange([start, ]
stop[, step,], dtype = None)

대괄호([]) 안의 값은 생략 가능한 값으로, 사용법이 python 의 range() 와 비슷하다.

start: 시작 값(기본값은 0)
stop: 끝 값(이 값은 포함되지 않음)
step: 간격(기본값은 1)
dtype: 결과 ndarray 의 데이터 타입

이 함수는 아래와 같이 사용한다.

  
np.arange(10)  # [0 1 2 3 4 5 6 7 8 9]
np.arange(10, 20)  # [10 11 12 13 14 15 16 17 18 19]
np.arange(10, 20, 5)  # [10 15]
np.arange(10, 20, 5, dtype=np.float64)  # [10. 15.]
np.arange(0, 1, 0.2)  # [0.  0.2 0.4 0.6 0.8]

linspace 로 ndarray 만들기

linearly spaced 의 줄임말로, N 등분한 숫자로 1 차원 ndarray 를 만들어준다.

함수 프로토타입은 아래와 같다.

  
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)

arange 와 달리 매개변수가 매우 많은데, 주요 매개변수는 아래와 같다.

start: 시퀀스의 시작 값
stop: 시퀀스의 끝 값
num: 생성할 샘플의 개수 (기본값: 50)
endpoint: True이면 stop을 포함, False이면 제외 (기본값: True)
retstep: True이면 샘플 간격도 함께 반환 (기본값: False)
dtype: 출력 배열의 데이터 타입
axis: 출력 배열에서 값들이 위치할 축 (기본값: 0)

이 함수는 아래와 같이 사용한다.

  
np.linspace(10, 20)  # 10부터 20까지를 50 등분한 1차원 ndarray 
np.linspace(10, 20, 5)  # [10.  12.5 15.  17.5 20. ]
np.linspace(10, 20, 5, dtype=np.int64)  # [10 12 15 17 20]

그럼 언제 arange 와 linspace 의 차이와 언제 어떤 것을 사용하면 좋을까?

특성	arange	linspace
지정 방식	간격(step) 지정	개수(num) 지정
끝점	포함하지 않음	기본적으로 포함
정밀도	부동소수점 오차 발생 가능	정확한 균등 분할

위와 같은 차이점이 있기 때문에, 적합한 사용 상황은 아래와 같이 달라 질 수 있다.

arange 는,
- 정수 범위를 생성할 때 (예: 0, 1, 2, …, 9)
- 정확한 간격을 알고 있을 때
- 간단한 인덱싱이나 반복에 사용할 때
linspace 는,
- 시작점과 끝점을 모두 포함해야 할 때
- 정확한 개수의 샘플이 필요할 때
- 그래프 플로팅이나 수치 적분 같은 과학적 계산에서
- 부동소수점 연산에서 정밀도가 중요할 때

즉, 정수나 정확한 간격을 알고 있을 때는 arange를, 시작과 끝점 사이의 **정확한** 개수의 균등한 값이 필요할 때는 linspace를 사용하는 것이 좋다.

✖️연산하기

기본적으로 Element Wise 연산을 하며, dtype 이 다르다면, 자동 형 변환(int → float → complex)이 된다.

Element Wise 연산

정의: 배열의 각 요소에 독립적으로 같은 연산을 적용하는 방식
기본 원칙: 두 배열 간 연산을 할 때 같은 위치의 요소끼리 연산함
필요 조건: 기본적으로 두 배열의 형태(shape)가 동일해야 함

Broadcasting

다른 형태의 배열 간 연산을 위해 사용되는 기능. 즉, 크기가 다른 배열 간에도 Element Wise 연산을 가능하게 하는 메커니즘
규칙(순서대로 적용)
1. 차원 맞추기: 차원 수가 적은 배열에, 1을 추가하여 차원 수를 맞춤
2. 각 차원 요소 크기 비교: 각 차원에서 크기가 같거나, 한 쪽이 1이어야 함
3. 크기가 1인 차원을 확장: 크기가 1인 차원을 다른 배열의 해당 차원 크기로 복사
규칙 3의 ”확장”이란, 크기가 1인 차원의 요소를 필요한 만큼 복사하여 배열 크기를 맞춘다는 의미
- 실제 메모리에 새 배열을 만들지 않고, 연산 시에만 확장된 것처럼 처리

주로 사용하는 연산

산술 연산자: +, -, *, /, **, %, //

  
import numpy as np

a = np.array([20, 30, 40, 50])
b = np.arange(4)  # [0, 1, 2, 3]

a + b  # [20, 31, 42, 53]
a - b  # [20, 29, 38, 47]
a * b  # [0, 30, 80, 150]
a * 10  # [200, 300, 400, 500]
b ** 2  # [0, 1, 4, 9]
b % 2  # [0, 1, 0, 1]
b // 2  # [0, 0, 1, 1]

비교 연산자: ==, !=, >, <, >=, <=

  
import numpy as np

a = np.array([20, 30, 40, 50])

a == 40  # [False, False, True, False]
a != 50  # [True, True, True, False]
a > 10  # [True, True, True, True]
a < 20  # [False, False, False, False]
a >= 40  # [False, False, True, True]
a <= 30  # [True, True, False, False]

논리 연산자: &, |, ~

  
import numpy as np

a = np.array([20, 30, 40, 50])

(a == 40) | (a == 50)  # [False, False,  True,  True]
(a % 2 == 0) & (a % 3 == 0)  # [False,  True, False, False]
~(a > 10)  # [False, False, False, False]

@: 행렬 곱셈(Matrix Product)

  
import numpy as np

A = np.array([[1, 1],
              [0, 1]])
B = np.array([[2, 0],
              [3, 4]])

A @ B  # [[5, 4], [3, 4]]

np.sum(): 모든 요소의 합

  
import numpy as np

# 1차원 배열
arr1 = np.array([1, 2, 3, 4, 5])
print(np.sum(arr1))  # 출력: 15

# 2차원 배열
arr2 = np.array([[1, 2, 3], [4, 5, 6]])
print(np.sum(arr2))  # 출력: 21
print(np.sum(arr2, axis=0))  # 열 방향 합계: [5, 7, 9]
print(np.sum(arr2, axis=1))  # 행 방향 합계: [6, 15]

# 메서드 형식으로도 사용 가능
print(arr2.sum())  # 출력: 21

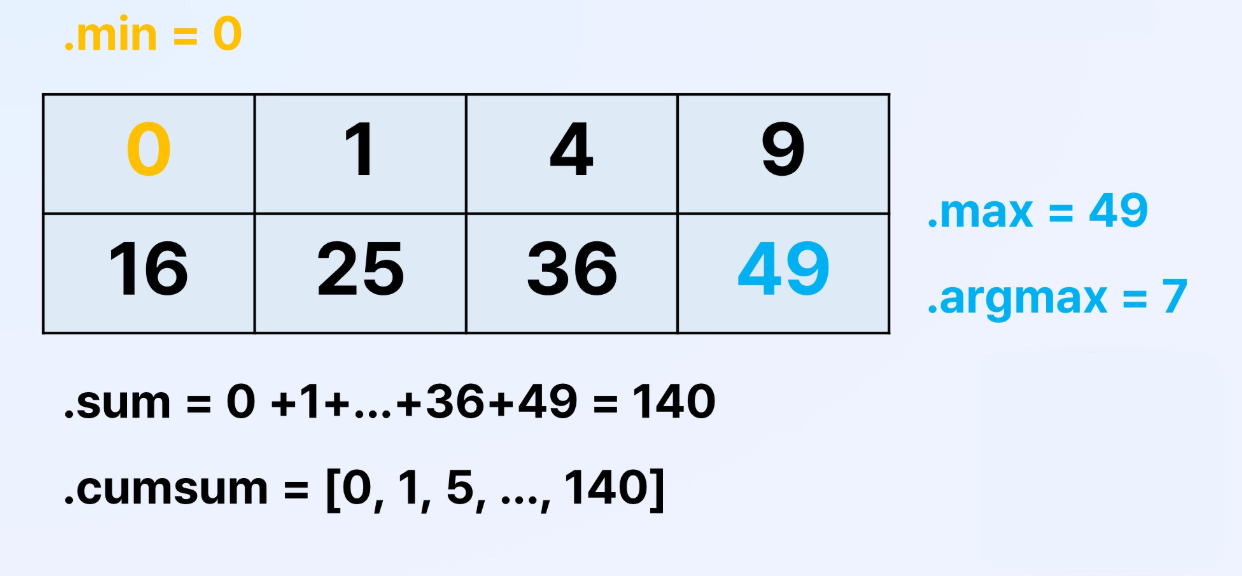
np.min(): 모든 요소 중 최소값

  
import numpy as np

# 1차원 배열
arr1 = np.array([5, 2, 8, 1, 9])
print(np.min(arr1))  # 출력: 1

# 2차원 배열
arr2 = np.array([[3, 1, 7], [4, 5, 2]])
print(np.min(arr2))  # 출력: 1
print(np.min(arr2, axis=0))  # 열 방향 최소값: [3, 1, 2]
print(np.min(arr2, axis=1))  # 행 방향 최소값: [1, 2]

# 메서드 형식으로도 사용 가능
print(arr2.min())  # 출력: 1

np.max(): 모든 요소 중 최대값

  
import numpy as np

# 1차원 배열
arr1 = np.array([5, 2, 8, 1, 9])
print(np.max(arr1))  # 출력: 9

# 2차원 배열
arr2 = np.array([[3, 1, 7], [4, 5, 2]])
print(np.max(arr2))  # 출력: 7
print(np.max(arr2, axis=0))  # 열 방향 최대값: [4, 5, 7]
print(np.max(arr2, axis=1))  # 행 방향 최대값: [7, 5]

# 메서드 형식으로도 사용 가능
print(arr2.max())  # 출력: 7

np.argmax(): 모든 요소 중 최대값의 인덱스
- 중요 동작 방식
  - axis=None일 경우: 배열을 평탄화(flatten)하여 1차원으로 변환한 후, 전체 배열에서 최대값의 인덱스를 단일 값으로 반환한다.
  - axis가 지정된 경우: 지정된 축을 따라 최대값을 찾으며, 각 슬라이스에서 최대값의 해당 축 인덱스를 반환한다. 결과 배열의 형태는 입력 배열에서 지정한 축이 제거된 형태이다.

  
import numpy as np

# 1차원 배열
arr1 = np.array([5, 2, 8, 1, 9])
print(np.argmax(arr1))  # 출력: 4 (9가 위치한 인덱스)

# 2차원 배열
arr2 = np.array([[3, 1, 7], [4, 5, 2]])

# axis=None (기본값): 배열을 평탄화한 후 최대값의 인덱스 반환
# 평탄화된 배열: [3, 1, 7, 4, 5, 2]
print(np.argmax(arr2))  # 출력: 2 (7의 인덱스)

# axis=0 (열 방향): 각 열에서 최대값의 인덱스 반환
# 0열: [3, 4] -> 최대값 4의 인덱스는 1
# 1열: [1, 5] -> 최대값 5의 인덱스는 1
# 2열: [7, 2] -> 최대값 7의 인덱스는 0
print(np.argmax(arr2, axis=0))  # 출력: [1, 1, 0]

# axis=1 (행 방향): 각 행에서 최대값의 인덱스 반환
# 0행: [3, 1, 7] -> 최대값 7의 인덱스는 2
# 1행: [4, 5, 2] -> 최대값 5의 인덱스는 1
print(np.argmax(arr2, axis=1))  # 출력: [2, 1]

# 메서드 형식으로도 사용 가능
print(arr2.argmax())  # 출력: 2

# 3차원 배열 (2x3x4)
arr3d = np.array([[[1, 2, 3, 4],
                   [5, 6, 7, 8],
                   [9, 10, 11, 12]],

                  [[13, 14, 15, 16],
                   [17, 18, 19, 20],
                   [21, 22, 23, 24]]])

# axis=None: 평탄화된 배열에서 최대값의 인덱스
print(np.argmax(arr3d))  # 출력: 23 (값 24의 인덱스)

# axis=0: 첫 번째 축(깊이)을 따라 최대값의 인덱스
# 결과 형태: (3, 4) -> 각 (행, 열) 위치에서 깊이 방향 최대값의 인덱스
print(np.argmax(arr3d, axis=0))
# 출력:
# [[1 1 1 1]
#  [1 1 1 1]
#  [1 1 1 1]]

# axis=1: 두 번째 축(행)을 따라 최대값의 인덱스
# 결과 형태: (2, 4) -> 각 (깊이, 열) 위치에서 행 방향 최대값의 인덱스
print(np.argmax(arr3d, axis=1))
# 출력:
# [[2 2 2 2]
#  [2 2 2 2]]

# axis=2: 세 번째 축(열)을 따라 최대값의 인덱스
# 결과 형태: (2, 3) -> 각 (깊이, 행) 위치에서 열 방향 최대값의 인덱스
print(np.argmax(arr3d, axis=2))
# 출력:
# [[3 3 3]
#  [3 3 3]]

np.cumsum(): 모든 요소의 누적합

  
import numpy as np

# 1차원 배열
arr1 = np.array([1, 2, 3, 4, 5])
print(np.cumsum(arr1))  # 출력: [1, 3, 6, 10, 15]

# 2차원 배열
arr2 = np.array([[1, 2, 3], [4, 5, 6]])
print(np.cumsum(arr2))  # 평탄화된 누적합: [1, 3, 6, 10, 15, 21]
print(np.cumsum(arr2, axis=0))  # 열 방향 누적합: [[1, 2, 3], [5, 7, 9]]
print(np.cumsum(arr2, axis=1))  # 행 방향 누적합: [[1, 3, 6], [4, 9, 15]]

# 메서드 형식으로도 사용 가능
print(arr2.cumsum())  # 출력: [1, 3, 6, 10, 15, 21]

범용 함수

매우 많은 함수를 NumPy 에서 제공하고 있기때문에 공식 문서를 한번 살펴 보는 것이 좋다.

공식 문서를 간략히 정리해보면 아래와 같다.

수학 연산 함수
- add(x1, x2): 요소별 덧셈 연산을 수행한다.
- subtract(x1, x2): 요소별 뺄셈 연산을 수행한다.
- multiply(x1, x2): 요소별 곱셈 연산을 수행한다.
- divide(x1, x2): 요소별 실수 나눗셈 연산을 수행한다.
- power(x1, x2): 첫 번째 배열의 요소를 두 번째 배열의 요소만큼 거듭제곱한다.
- sqrt(x): 요소별 제곱근을 계산한다.
- square(x): 요소별 제곱을 계산한다.
- absolute(x): 요소별 절대값을 계산한다.
- exp(x): 요소별 지수 함수(e^x)를 계산한다.
- log(x): 요소별 자연로그를 계산한다.
- log10(x): 요소별 밑이 10인 로그를 계산한다.
삼각 함수
- sin(x): 요소별 사인(sine) 함수를 계산한다.
- cos(x): 요소별 코사인(cosine) 함수를 계산한다.
- tan(x): 요소별 탄젠트(tangent) 함수를 계산한다.
- arcsin(x): 요소별 아크사인(역사인) 함수를 계산한다.
- arccos(x): 요소별 아크코사인(역코사인) 함수를 계산한다.
- arctan(x): 요소별 아크탄젠트(역탄젠트) 함수를 계산한다
- deg2rad(x): 각도를 도(degree)에서 라디안(radian)으로 변환한다.
- rad2deg(x): 각도를 라디안(radian)에서 도(degree)로 변환한다.
비트 연산 함수
- bitwise_and(x1, x2): 요소별 비트 AND 연산을 수행한다.
- bitwise_or(x1, x2): 요소별 비트 OR 연산을 수행한다.
- bitwise_xor(x1, x2): 요소별 비트 XOR 연산을 수행한다.
- invert(x): 요소별 비트 NOT 연산을 수행한다.
비교 함수
- greater(x1, x2): 요소별로 x1 > x2 비교하여 부울 배열을 반환한다.
- greater_equal(x1, x2): 요소별로 x1 >= x2 비교하여 부울 배열을 반환한다.
- less(x1, x2): 요소별로 x1 < x2 비교하여 부울 배열을 반환한다.
- less_equal(x1, x2): 요소별로 x1 <= x2 비교하여 부울 배열을 반환한다.
- equal(x1, x2): 요소별로 x1 == x2 비교하여 부울 배열을 반환한다.
- not_equal(x1, x2): 요소별로 x1 != x2 비교하여 부울 배열을 반환한다.
논리 함수
- logical_and(x1, x2): 요소별 논리 AND 연산을 수행한다.
- logical_or(x1, x2): 요소별 논리 OR 연산을 수행한다.
- logical_not(x): 요소별 논리 NOT 연산을 수행한다.
최대/최소 함수
- maximum(x1, x2): 두 배열의 요소별 최대값을 반환한다.
- minimum(x1, x2): 두 배열의 요소별 최소값을 반환한다.
부동소수점 관련 함수
- isfinite(x): 요소가 유한수인지 테스트한다.
- isinf(x): 요소가 무한대인지 테스트한다.
- isnan(x): 요소가 NaN(Not a Number)인지 테스트한다.
- floor(x): 요소별로 내림(floor) 연산을 수행한다.
- ceil(x): 요소별로 올림(ceiling) 연산을 수행한다.
- trunc(x): 요소별로 소수점 이하를 버림(truncate) 연산을 수행한다.
팁
- 출력 인수 옵션(out)을 사용하면 큰 계산에서 메모리를 절약할 수 있다.
- 복잡한 표현식의 경우 G = a * b + c 대신 G = a * b; add(G, c, G)와 같이 사용하면 임시 계산 공간을 줄여 성능이 향상된다.
- 논리 연산시 파이썬 키워드 and와 or 대신 비트 연산자 &와 |를 사용해야 요소별 연산이 수행된다.

🍕 Indexing 과 Slicing

NumPy 는 배열은 강력한 인덱싱과 슬라이싱 기능을 제공하여 데이터 접근과 조작을 효율적으로 할 수 있게한다.

기본 인덱싱과 슬라이싱

기본적으로는 python 의 list 나 tuple 에서의 indexing 과 같다.

  
import numpy as np

a = np.arange(10) ** 2  # [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

# a 배열의 2번째 인덱스 출력
a[2]  # 결과: 4 (인덱스 2의 값)

# a 배열의 2~4번 인덱스 출력
a[2:5]  # 결과: array([4, 9, 16]) (인덱스 2부터 4까지)

# reverse : 배열의 요소 거꾸로 출력
a[::-1]  # 결과: array([81, 64, 49, 36, 25, 16, 9, 4, 1, 0]) (모든 요소를 역순으로)

슬라이싱을 통한 배열 수정

NumPy 배열의 슬라이싱은 뷰(View) 를 반환하므로, 슬라이스를 수정하면 원본 배열도 수정된다.
- View: (View 와 Copy 의 차이 참고
즉, 슬라이싱을 사용하여 배열의 특정 부분을 일괄적으로 변경할 수 있다.
a[:6:2] = 1000 와 같이 스칼라 값을 할당하면, 해당 스칼라 값이 선택된 모든 위치에 브로드캐스팅된다.
배열을 할당할 때는 슬라이스의 크기와 할당하는 배열의 크기가 일치해야한다.

  
import numpy as np

a = np.arange(10) ** 2  # [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

# 0~5번에서 2Step 인덱스 출력 (0, 2, 4 인덱스)
a[:6:2] = np.array([1000, 1000, 1000])
# a = [1000, 1, 1000, 9, 1000, 25, 36, 49, 64, 81]

# 인덱스 0, 2, 4에 해당하는 값에 모두 1000 삽입 (간소화된 방법)
a[:6:2] = 1000
# a = [1000, 1, 1000, 9, 1000, 25, 36, 49, 64, 81]

배열로 인덱싱(Fancy Indexing)

팬시 인덱싱(Fancy Indexing)은, NumPy 에서 배열을 사용하여 다른 배열의 요소에 접근하는 기술을 말한다.
임의의 인덱스 집합을 지정할 수 있어 더 유연하기 때문에 “멋진(fanch)” 방식으로 데이터를 선택할 수 있다는 의미에서 이런 이름이 붙었다. 실제 공식 문서에도 팬시 인덱싱(Fancy Indexing)이라는 용어를 사용한다.
팬시 인덱싱은 정수 배열을 사용하여 특정 인덱스 위치의 값들을 선택한다.
1차원 인덱스 배열을 사용할 때, 결과는 그 배열과 같은 형태를 가진다.
2차원 인덱스 배열을 사용할 때는, 결과도 그 2차원 형태를 가진다.
즉, 결과는 인덱스 배열과 같은 shape 가진다. (인덱싱 결과의 shape 은 인덱싱 배열의 shape에 의해 결정)
인덱스 배열에 중복된 인덱스가 있어도 동작한다.
팬시 인덱싱은 항상 원본 배열의 복사본을 반환(뷰가 아니다!)

  
import numpya as np

a = np.arange(8) ** 2  # [0, 1, 4, 9, 16, 25, 36, 49]

# i 1차원 배열 생성 & 출력
i = np.array([1, 1, 3, 5])  # [1, 1, 3, 5]

# a[i]는 a 배열에서 i의 인덱스에 해당하는 값들을 가져옴
a[i]  # 결과: array([1, 1, 9, 25]) (a의 1, 1, 3, 5 인덱스 값)

# j 2차원 배열 생성
j = np.array([[3, 4], [2, 5]])  # [[3 4],[2 5]]

# a 배열의 index로 j를 삽입하여 출력
indexed_a = a[j]
# 결과: array([[ 9, 16],
#              [ 4, 25]])

a.shape, indexed_a, indexed_a.shape
# 결과: ((8,), array([[ 9, 16], [ 4, 25]]), (2, 2))

불리언 인덱싱

조건식을 통해 True/False 배열을 생성하고, 이를 인덱스로 사용한다.
여러 조건을 결합할 때는 괄호와 논리 연산자를 사용한다.
불리언 인덱싱으로 선택된 요소들에 값을 할당하면 해당 위치만 업데이트된다.

  
import numpy as np

a = np.arange(12).reshape(3, 4)  # 3x4 행렬 생성
# 결과:
# [[ 0  1  2  3]
#  [ 4  5  6  7]
#  [ 8  9 10 11]]

# b는 a > 4 조건이 적용된 Boolean 값이 든 배열
b = a > 4
b  # 결과: array([[False, False, False, False],
#             [False,  True,  True,  True],
#             [ True,  True,  True,  True]])

# Boolean 값이 든 b 배열을 a 배열의 index로 삽입
# True인 값들만 출력
a[b]  # 결과: array([ 5,  6,  7,  8,  9, 10, 11]) (a에서 4보다 큰 모든 값)

# a[b]에 해당하는 애들만 0 삽입하여 a 출력
a[b] = 0
a  # 결과: array([[ 0,  1,  2,  3],
#             [ 4,  0,  0,  0],
#             [ 0,  0,  0,  0]])

다차원 배열의 인덱싱

다차원 배열에서 각 차원의 인덱스를 콤마로 구분하여 지정한다.
한 차원에 대해 모든 인덱스를 선택하려면 : 을 사용한다.
단일 인덱스로 행을 선택하면 해당 행의 1차원 배열이 반환된다.
특정 요소 접근 시 각 차원의 인덱스를 순서대로 지정한다.
행과 열 모두 슬라이싱을 적용하여 부분 행렬을 선택할 수 있다.

  
import numpy as np

# 2차원 배열 생성
matrix = np.arange(12).reshape(3, 4)
"""
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
"""

# 행 인덱싱
row_1 = matrix[1]  # array([4, 5, 6, 7])

# 열 인덱싱
col_2 = matrix[:, 2]  # array([2, 6, 10])

# 특정 요소 인덱싱
element = matrix[1, 2]  # 6

# 부분 행렬 선택
sub_matrix = matrix[0:2, 1:3]
"""
array([[1, 2],
       [5, 6]])
"""

View 와 Copy 의 차이

NumPy 배열의 View란 원본 배열의 데이터를 새로운 메모리에 복사하지 않고, 동일한 메모리 공간을 참조하는 새로운 배열 객체를 의미한다.

View (뷰)
- 원본 배열과 동일한 데이터를 공유한다.
- 메모리 추가 할당 없이 데이터를 참조한다.
- View를 수정하면 원본 배열도 변경된다.
- 슬라이싱 연산 (arr[1:5])은 View를 반환한다.
Copy (복사본):
- 원본 배열의 데이터를 완전히 새로운 메모리 공간에 복사한다.
- 원본 배열과 독립적이다.
- 복사본을 수정해도 원본에 영향을 주지 않는다.
- .copy() 메서드나 특정 연산으로 생성된다.

NumPy 배열을 슬라이싱하면 View가 반환되고, 인덱싱을 하면 복사본이 반환된다.

하지만 a[a < 4] = 0 과 같은 코드가 원본 배열을 수정할 수 있는 이유는, NumPy 가 이 경우에 특별한 처리를 하기 때문이다. 좌변에서의 인덱싱(할당 대상으로서)과 우변에서의 인덱싱(값을 가져오는 용도로서)이 다르게 동작도록 구현되어있는 것이다.

정리하면 다음과 같다.

슬라이싱: View를 반환하므로 수정 시 원본 배열도 변경된다.
팬시 인덱싱(배열로 인덱싱): 복사본을 반환하므로 수정해도 원본에 영향이 없다.
불리언 인덱싱: 복사본을 반환하지만, 좌변에서 사용될 때는 원본 배열의 해당 위치를 직접 수정한다.

✨ shape 변경하기

배열의 차원과 형태를 변경하는 여러 방법 중, ravel, reshape, T 에 대해서 알아보겠다.

ravel()

풀어헤치다, 펼치다는 의미의 영단어인 만큼 N 차원의 배열을 1차원 배열로 평탄화(flatten)한다.
View를 반환한다.

  
import numpy as np

# 2차원 배열 생성
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
print(arr_2d)
# [[1 2 3]
#  [4 5 6]]

# ravel()을 사용하여 1차원으로 평탄화
flat_arr = arr_2d.ravel()
print(flat_arr)
# [1 2 3 4 5 6]

reshape()

re(다시) + shape(모양) 의 합성어로, 배열의 모양을 다시 구성한다.
차원과 형태를 재구성하는 것으로, 일반적으로 View를 반환하지만 메모리 레이아웃이 연속하지 않을 경우 Copy를 반환할 수 있다.
전체 요소 수는 변경 전후가 같아야 한다.
-1 을 사용하여 자동 계산되는 차원을 지정할 수 있으며, reshape(-1) 은 1차원으로 평탄화하는 것이다.

  
import numpy as np

# 1차원 배열 생성
arr_1d = np.arange(12)  # [0  1  2  3  4  5  6  7  8  9 10 11]
print(arr_1d)  # [0  1  2  3  4  5  6  7  8  9 10 11]

# 2차원 배열로 reshape
arr_2d = arr_1d.reshape(4, 3)
print(arr_2d)
# [[ 0  1  2]
#  [ 3  4  5]
#  [ 6  7  8]
#  [ 9 10 11]]

# 3차원 배열로 reshape
arr_3d = arr_1d.reshape(2, 2, 3)
print(arr_3d)
# [[[ 0  1  2]
#   [ 3  4  5]]
#  [[ 6  7  8]
#   [ 9 10 11]]]

# 원본 배열 변경
arr_1d[0] = 100
print(arr_1d)  # [100   1   2   3   4   5   6   7   8   9  10  11]

# reshape된 배열들에도 변경이 반영됨 (view이므로)
print(arr_2d)
# [[100   1   2]
#  [  3   4   5]
#  [  6   7   8]
#  [  9  10  11]]

print(arr_3d)
# [[[100   1   2]
#   [  3   4   5]]
#  [[  6   7   8]
#   [  9  10  11]]]

# 2차원 배열 변경
arr_2d[1, 1] = 999
print(arr_2d)
# [[100   1   2]
#  [  3 999   5]
#  [  6   7   8]
#  [  9  10  11]]

# 1차원 및 3차원 배열에도 변경이 반영됨
print(arr_1d)  # [100   1   2   3 999   5   6   7   8   9  10  11]
print(arr_3d)
# [[[100   1   2]
#   [  3 999   5]]
#  [[  6   7   8]
#   [  9  10  11]]]

T(Transpose)

선형대수학에서의 행렬 전치를 의미한다.
배열의 축(axis)을 반전시킨다. 즉, 2차원 배열에서 행과 열을 교환한다.
T 는 속성(property)으로, 메서드가 아니다.
다차원 배열에서는 모든 축의 순서가 반전된다.(예: (i, j, k) → (k, j, i))
1차원은 전치해도 그대로 1차원 배열이다.
항상 View를 반환한다.

  
import numpy as np

matrix = np.array([[1, 2, 3], [4, 5, 6]])
print(matrix)
# [[1 2 3]
#  [4 5 6]]

# 전치행렬 구하기
transposed = matrix.T
print(transposed)
# [[1 4]
#  [2 5]
#  [3 6]]

# 3차원 배열 생성
array_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print(array_3d)
# [[[1 2]
#   [3 4]]
#  [[5 6]
#   [7 8]]]
print("3차원 배열의 shape:", array_3d.shape)  # (2, 2, 2)

# 3차원 배열의 전치
transposed_3d = array_3d.T
print(transposed_3d)
# [[[1 5]
#   [3 7]]
#  [[2 6]
#   [4 8]]]
print("전치된 3차원 배열의 shape:", transposed_3d.shape)  # (2, 2, 2)

🪓 병합과 분할

np.vstack() - 수직 방향 결합 (Vertical Stack)

배열들을 수직 방향(위에서 아래로)으로 결합한다. 행(row)을 추가하는 형태로 결합된다.
모든 입력 배열은 동일한 열(column) 수를 가져야 한다.
1차원 배열은 행 벡터(row vector)로 취급된다.
결과는 항상 2차원 이상의 배열이다.

  
import numpy as np

# 예제 배열 생성
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 수직 방향으로 결합
result = np.vstack((a, b))
print(result)
# [[1 2 3]
#  [4 5 6]]

# 2차원 배열의 결합
c = np.array([[7, 8, 9], [10, 11, 12]])
result2 = np.vstack((result, c))
print(result2)
# [[ 1  2  3]
#  [ 4  5  6]
#  [ 7  8  9]
#  [10 11 12]]

np.hstack() - 수평 방향 결합 (Horizontal Stack)

배열들을 수평 방향(왼쪽에서 오른쪽으로)으로 결합한다. 열(column)을 추가하는 형태로 결합된다.
모든 입력 배열은 동일한 행(row) 수를 가져야 한다.
1차원 배열은 그대로 연결된다.
2차원 이상의 배열에서는 두 번째 축(axis=1)을 따라 결합된다.

  
import numpy as np

# 예제 배열 생성
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 수평 방향으로 결합
result = np.hstack((a, b))
print(result)  # [1 2 3 4 5 6]

# 2차원 배열의 결합
c = np.array([[1, 2], [3, 4]])
d = np.array([[5, 6], [7, 8]])
result2 = np.hstack((c, d))
print(result2)
# [[1 2 5 6]
#  [3 4 7 8]]

np.hsplit() - 수평 방향 분할 (Horizontal Split)

배열을 수평 방향(왼쪽에서 오른쪽으로)으로 여러 부분으로 분할한다.
배열을 지정된 수의 하위 배열로 나누거나, 지정된 인덱스(위치)에서 분할할 수 있다.
인덱스 목록을 전달하면, 해당 위치들을 기준으로 분할한다.
분할 개수는 배열의 크기에 맞게 균등하게 나눌 수 있어야 하며, 그렇지 않으면 오류가 발생한다.

  
import numpy as np

# 예제 배열 생성
a = np.array([1, 2, 3, 4, 5, 6])

# 3개의 균등한 부분으로 분할
result = np.hsplit(a, 3)
print(result)
# [array([1, 2]), array([3, 4]), array([5, 6])]

# 2차원 배열 분할
b = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])

# 2개의 균등한 부분으로 분할
result2 = np.hsplit(b, 2)
print(result2)
# [array([[1, 2],
#         [5, 6]]), array([[3, 4],
#                          [7, 8]])]

# 인덱스를 기준으로 분할
result3 = np.hsplit(b, [1, 3])
print(result3)
# [array([[1],
#         [5]]), array([[2, 3],
#                      [6, 7]]), array([[4],
#                                      [8]])]

np.vsplit() - 수직 방향 분할

hsplit()과 대응되는 vsplit() 함수도 있어 수직 방향(위에서 아래로)으로 배열을 분할할 수 있다.

  
import numpy as np

# 예제 배열 생성
b = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

# 2개의 균등한 부분으로 수직 분할
result = np.vsplit(b, 2)
print(result)
# [array([[1, 2, 3],
#         [4, 5, 6]]), array([[ 7,  8,  9],
#                            [10, 11, 12]])]

# 인덱스를 기준으로 수직 분할
result2 = np.vsplit(b, [1, 3])
print(result2)
# [array([[1, 2, 3]]), array([[4, 5, 6],
#                            [7, 8, 9]]), array([[10, 11, 12]])]

1.TIL, 1-2.PYTHON

python numpy

This post is licensed under CC BY 4.0 by the author.